Graph-Theoretic Methods and Applications
Overview
Graph-based codes are extremely popular due to their excellent performance in a variety of settings and relative ease of implementations. In the asymptotic setting, certain simplifying and averaging assumptions apply; this equips us with the ability to apply celebrated density evolution-like techniques. In contrast, finite-length code performance has been plagued by the mathematical sub optimality of the associated message passing decoders. In this setting, conventional code optimization methods are not adequate.
In this research, we tackle both domains. We develop a comprehensive theoretical analysis of several structured code families using tools from enumerative combinatorics, combinatorial graph theory, and matrix analysis. In the finite-length case in particular, we create a new code design methodology centered on the analysis of small graphical constructs that govern code performance in the high reliability regime. Our approach succinctly describes these problematic objects and offers principled ways of eliminating them; our mathematical machinery offers provable properties for the entire finite-length code family at once and thus enables system engineers to use designed codes with confidence. Furthermore, we use this methodology to develop low-cost decoder hardware implementations.
Recent results
In our recent work, we have developed a new combinatorial framework for the analysis and design of finite-length spatially (SC) coupled codes. In particular, we have demonstrated that SC codes have superior properties to their LDPC counterparts in terms of code performance, by virtue of provably having fewer detrimental absorbing sets.
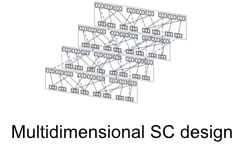
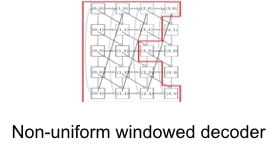
Current research focuses on extending our combinatorial machinery to a variety of channels, on analysis and design of multi-dimensional graph based codes suitable for ultra dense storage, and on the design of low-latency windowed decoders.
Recent Publications:
- L. Tauz, H. Esfahanizadeh, and L. Dolecek, “Non-Uniform Window Decoding for Multi-Dimensional Spatially-Coupled LDPC Codes,” in Proc. IEEE International Symposium onInformation Theory (ISIT), Los Angeles, CA, Jun. 2020.
- A. Hareedy, R. Wu, and L. Dolecek, “A Channel-Aware Combinatorial Approach to DesignHigh Performance Spatially-Coupled Codes for Magnetic Recording Systems,” IEEE Transactions on Information Theory, vol. 66 (8), pp. 4834- 4852, Aug. 2020.
- H. Esfahanizadeh, L. Tauz, and L. Dolecek, “Multi-Dimensional Spatially-Coupled Code Design: Enhancing the Cycle Properties,” IEEE Transactions on Communications, vol. 68 (5), pp. 2653 — 2666, May 2020.
- A. Hareedy, C. Lanka, N. Guo, and L. Dolecek, “A Combinatorial Methodology for Optimizing Non-Binary Graph-Based Codes: Theoretical Analysis and Applications in Data Storage,” IEEE Transactions on Information Theory, vol. 65 (4), pp. 2128 – 2154, Apr. 2019. IEEE Data Storage Society 2019 Best Student Paper Award.
- H. Esfahanizadeh, A. Hareedy, and L. Dolecek, “Finite-Length Construction of High Performance Spatially-Coupled Codes via Optimized Partitioning and Lifting,” IEEE Transactions on Communications, vol. 67(1), pp. 3-16, Jan. 2019.
- H. Esfahanizadeh, A. Hareedy, and L. Dolecek, “Spatially-Coupled Codes Optimized for Magnetic Recording Applications,” IEEE Transactions on Magnetics, vol. 53 (2), pp. 1 — 11, Feb. 2017.