Mathematical Foundations of Modern Computing

Overview

Modern computing systems must process large quantities of data quickly and efficiently. Scaling of the underlying devices is already at the level where simple techniques such as guard banding and replication are too resource intensive. Additionally, some applications may not even need perfect computations to produce outputs of acceptable quality (e.g., images). In this research, we establish the fundamental performance limits of computational systems built out of noisy components, and offer novel mathematical techniques to effectively mitigate the adverse effects of hardware noise while maintaining target quality.

In this work, we explore and formalize an untapped potential of a variety of mathematical techniques as well as intrinsic robustness of iterative algorithms to offer low-cost solutions for computing systems built out of unreliable components.

Recent results

Noisy and Approximate Computing

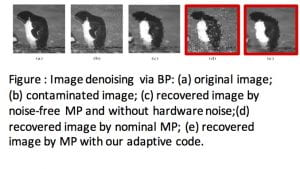We previously developed a comprehensive framework for the analysis and design of in the presence of computational noise, using variety of tools from probability theory, combinatorics, and information theory. Applications include several LDPC iterative decoders, signal processing, image denoising, and machine learning algorithms. We have proposed algorithm-assisted techniques for the recovery from hardware noise. Using tools from source and channel coding, we have also developed novel message shaping methods that in an algorithm-aware way minimize the effects of hardware noise, with applications to approximate computing. Additionally, we investigated the application of noisy computing to deep space applications to offset the high cost of device shielding and applications for fast in-memory computing.iterative algorithms

In-Memory Computing

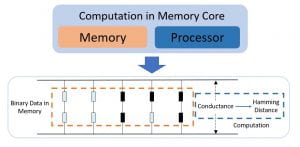
Enabled by new storage mediums, Computation-in-Memory is a 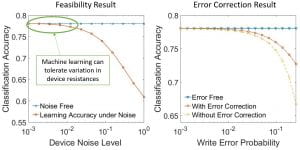novel architecture that has shown great potential in reducing the burden of massive data processing by bypassing the communication and memory access bottleneck. Allowing for ultra-fast Hamming distance computations to be performed in resistive memory with low-level conductance measurements has the potential to drastically speed up many modern machine learning algorithms.

First, we introduced a technique for estimating the Hamming distance under resistance variation alone. Then, we proposed error-detection and error-correction schemes to deal with non-ideal write process. We then combined these results to concurrently address both sources of memristor variabilities. In order to preserve the low latency property of Computation-in-Memory, all of our approaches rely on only a single vector-level conductance measurement. We use so-called inversion coding as a key ingredient in our solutions and we prove the optimality of this code given the restrictions on bit-accessible information. Lastly, we demonstrate the efficacy of our approaches on the k-nearest neighbors classifier.