Sequence Analysis and DNA Storage

Overview

Data reconstruction from traces is an important problem with numerous applications, including data recovery, genomics and other areas of biology, chemistry, sensor networks, associative memories, and many others. The general problem of reconstruction is broadly divided into probabilistic and adversarial variants. In the probabilistic version, the traces are formed by passing the data through a noisy channel (typically an edit channel with certain deletion and insertion probabilities) and the goal is to reconstruct the data to within a certain error probability.

Specifically, consider the problem of passing a sequence through a noisy channel multiple times, and trying to reconstruct the sequence from the set of distinct channel outputs. It is then of practical interest to know how many distinct channel outputs are required to reconstruct the sequence in the worst case, and furthermore, what is the most efficient algorithm to reconstruct.

For example, one goal in Phylogenomics is to recover genetic information of a deceased individual from the genetic information of its descendants. Here, the genetic information of each descendant can be viewed as a transmission of the ancestor’s genetic information through a noisy channel. The same questions can be asked: How many descendants are required to recover the ancestor’s information? How can we efficiently reconstruct the ancestor’s information?

Recent results

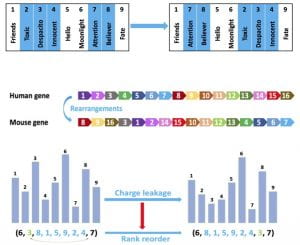
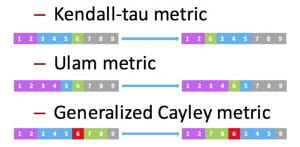Permutation codes have recently garnered substantial research interest due to their potential in various applications, including cloud storage systems, genome resequencing, and flash memories. The generalized Cayley metric captures the number of generalized transposition errors in a permutation and subsumes previously studied error types, including transpositions and translocations, without imposing restrictions on the lengths and positions of the translocated segments. We developed a coding framework that leads to order-optimal constructions, thus improving upon the existing constructions that are not order-optimal. We then used this framework to also develop an order-optimal coding scheme that is additionally explicit and systematic.

We recently found a closed form for the number of distinct insertion-channel outputs required to reconstruct, when the possible original sequences are separated by some minimum edit distance. This is useful for insertion correcting-codes where all codewords are separated by some edit distance.   It is also relevant to Phylogenomics because potential ancestors likely have genetic information that is separated by some non-trivial edit distance. We have several other novel results in submission and in preparation. Current research also involves specializing our framework to DNA storage.

Recent Publications:

• S. Yang, C. Schoeny, and L. Dolecek, “Theoretical Bounds and Constructions of Codes in the Generalized Cayley Metric,” IEEE Transactions on Information Theory, vol. 65 (8), pp. 4746– 4763, Aug. 2019.
• L. Conde-Canencia and L. Dolecek, “Nanopore DNA Sequencing Channel Modeling,” in Proc. IEEE Workshop on Signal Processing Systems (SiPS), Cape Town, South Africa, Oct. 2018.
• F. Sala, R. Gabrys, C. Schoeny, and L. Dolecek, “Exact Reconstruction from Insertions in Synchronization Codes,” IEEE Transactions on Information Theory, vol. 63 (4), pp. 2428 — 2446, April 2017.